I recently purchased a second-hand 10-18 mm wide angle lens for my DSLR. Measuring its vignetting using my previous method is difficult as it has a field of view in excess of 100°. It's hard to provide an evenly illuminated target this large. The answer is to assume the lens has no vignetting at its smallest aperture, and use an image at this aperture as a reference when measuring the vignetting.
I set up the camera on my dining room table with an A4 sheet of translucent Perspex (or similar) an inch or so in front of the lens hood. The camera was facing towards the window, but no other lighting was used.
This is a photo taken at 10mm focal length and maximum aperture, ƒ/4.5.

At minimum aperture, ƒ/22, the result doesn't look much different, apart from a bit of fluff on the front of the lens being more nearly in focus.

Dividing the ƒ/4.5 image by the ƒ/22 (after converting both to luminance) gives this image.

This may not appear to have much vignetting, but my analysis and curve fitting suggests otherwise.
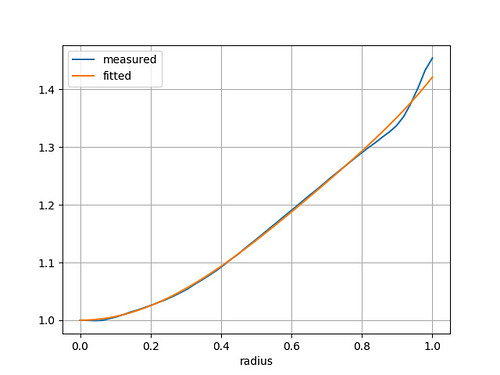
The fitted function (shown in orange) is a polynomial in r², r⁴, and r⁶. Using even powers of r ensures the function has zero slope at r=0. The correction required is about half an ƒ-stop (factor of 1.41) at the corners.
Running the process for narrower apertures shows the expected reduction in vignetting.
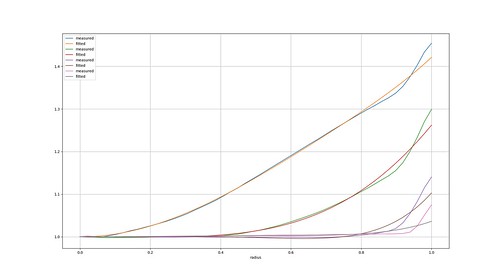
I think the "measured" curves show some similarity, but a 3rd order polynomial (in r²) is not a good match at smaller apertures. There's also no obvious trend in the polynomial coefficients, so I can't confidently predict the correction required at other apertures. I'd like to find a better fitting function, but I think this is beyond my mathematical abilities.
PS I've just tried fitting a power function
1.0 + (a * (x ** b)) instead of a polynomial and instantly got better looking results.
No comments:
Post a Comment